Modelos caóticos de baja dimensión para la micro-atmósfera de la cueva prehistórica de Altamira (España)
La aplicación de la técnica de modelización global a la micro-atmósfera de la cueva de Altamira ha permitido obtener modelos caóticos de baja dimensión a partir de las variaciones en su contenido de dióxido de carbono (CO2) y radón (222Rn), las cuales resultan de la actividad biológica del suelo y de un proceso físico de desintegración, respectivamente. El análisis cruzado de los datos ha permitido destacar el acoplamiento de la atmósfera de la cueva con el contenido de agua del suelo situado en la superficie, directamente encima de la cavidad: el agua del suelo obstaculiza los intercambios de gas durante la estación húmeda, mientras que durante la estación seca la disminución en el contenido de humedad del suelo permite que los gases acumulados en la atmósfera de la cueva escapen al exterior.
Todos sabemos que el comportamiento de la atmósfera a veces es difícil de predecir. Para comprender las causas fundamentales de este comportamiento, en la década de 1960 el meteorólogo Barry Saltzman intentó describir la dinámica de la atmósfera mediante un pequeño número de variables[i]. Posteriormente, Edward N. Lorenz simplificó este modelo y publicó en 1963[ii] el primer modelo caótico de baja dimensión: completamente determinista pero impredecible a largo plazo, a menos que se conozcan su formulación y su estado inicial con total exactitud. Demasiado simple para realizar pronósticos meteorológicos con él, este modelo permitió, sin embargo, mostrar que tres variables y un mínimo de no linealidad podían ser suficientes para producir este comportamiento determinista pero impredecible a largo plazo.
Gracias a una colaboración franco-hispana[iii], se ha analizado la atmósfera de la cueva de Altamira utilizando la técnica de modelización global, una técnica de modelización basada en la teoría del caos[iv]. Situada en la provincia de Cantabria, en el norte de España, la cueva de Altamira contiene una de las colecciones pictóricas más destacadas de finales del Paleolítico superior. Estuvo habitada durante varios milenios, hasta que la entrada a la cueva se derrumbó hace unos 13.000 años, aislando sus pinturas en un entorno estable que ha favorecido su conservación. La cueva, descubierta a finales del siglo XIX, fue declarada Patrimonio de la Humanidad por la UNESCO en 1985. Además, se empezó a monitorizar la atmósfera de la cueva para velar por la conservación de los polícromos y la seguridad de los visitantes.
En este estudio se han utilizado las concentraciones de dióxido de carbono (CO2) y radón (en concreto, el isótopo 222Rn por ser más estable) en la cueva y el contenido de agua del suelo, medidos en el período 2007-2012. El origen natural del CO2 y del radón se conoce con bastante certeza. Las moléculas de CO2 provienen principalmente de la actividad biológica (la respiración de organismos que viven en el suelo o en su superficie, como plantas y microorganismos), mientras que el isótopo 222Rn resulta de la desintegración de partículas de uranio contenidas naturalmente en suelos y rocas. Pero conocer la procedencia de estos dos componentes no permite explicar la evolución estacional de sus concentraciones, y menos aún si se considera que la cueva de Altamira presenta un funcionamiento opuesto al comúnmente observado en la mayoría de las cuevas de morfología semejante (con una ligera pendiente descendente). Por lo general, en esta configuración, el aire de la cueva permanece atrapado durante el verano porque es más frío y, por lo tanto, más denso que el de la atmósfera exterior. En consecuencia, no puede salir por las aberturas ubicadas en posiciones elevadas. Sin embargo, para la cueva de Altamira este comportamiento se invierte: es durante la estación fría cuando se acumulan CO2 y radón, y en verano cuando se produce la ventilación y bajan sus concentraciones, como se muestra en la Figura 1.
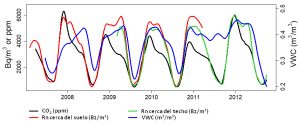
Figura 1: Serie temporal filtrada de la concentración de CO2 [en ppm] y radón 222Rn [en Bq / m3] en la micro-atmósfera de la cueva de Altamira (norte de España), en la sala de los Polícromos; contenido de agua del suelo situado sobre la cueva en la superficie [en m3/m3] (a 5 cm de profundidad).
Ya en 2008, se señalaron las variaciones en el contenido de agua del suelo como una posible explicación para este comportamiento[v]. La ventilación a través del techo de la cueva implica que los niveles situados por encima del mismo no están saturados de agua, por lo que permiten que los gases, previamente acumulados, se exhalen a la atmósfera exterior. Por el contrario, cuando hay agua en los intersticios del suelo y la roca, el intercambio de gases con el exterior puede verse gravemente obstaculizado y estos se acumulan en la micro-atmósfera de la cueva.
Iniciada en la década de 1990, la técnica de modelización global se desarrolló para estudiar comportamientos dinámicos a partir de una sola variable (una sola serie de medidas). En los últimos años, hemos podido demostrar que el enfoque se puede extender a pequeños conjuntos de variables, con el objetivo de recuperar la formulación original de las ecuaciones, o bien para obtener ecuaciones interpretables cuando se desconocen las ecuaciones originales[vi]. En este nuevo estudio, mostramos que el enfoque se puede utilizar para detectar acoplamientos direccionales entre variables, aun cuando no se dispone de observaciones de todas las variables esenciales.
El uso de la técnica de modelización global en este contexto ha permitido no solo obtener modelos de baja dimensión capaces de producir comportamientos caóticos, sino también probar la hipótesis de la participación del agua del suelo en este comportamiento atmosférico invertido[vii].
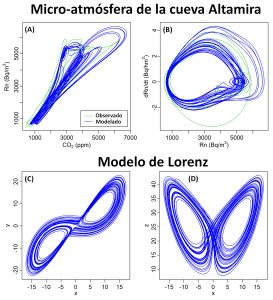
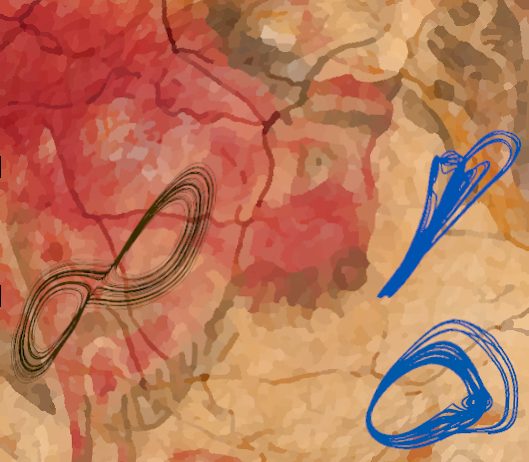
Figura 2: Arriba: atractor caótico de la micro-atmósfera de la cueva de Altamira. Se presentan dos proyecciones: concentración de radón (222Rn) en función de la concentración de CO2 (A), y velocidad de los cambios en la concentración de radón (dRn/dt) en función de la concentración de radón en sí (B). Las simulaciones (en azul) se superponen a los datos originales (en verde). Abajo: el atractor caótico de Lorenz visto siguiendo las proyecciones y en función de x (C), y z en función de x (D).
Se ha obtenido un modelo que acopla la concentración de radón a las variaciones en el contenido de agua del suelo. Con este modelo sólo se puede generar un régimen periódico, que por tanto no tiene en cuenta la complejidad observada. Sin embargo, aunque simplista, este modelo sigue siendo de interés porque ofrece un primer argumento dinámico sobre la importancia del papel del agua del suelo en la dinámica del intercambio de gases entre la atmósfera y la cueva. Además, el modelo puede reformularse en un modelo no autónomo: las mediciones del contenido de agua del suelo pueden usarse empíricamente como un forzamiento del modelo de la micro-atmósfera. Este resultado puede parecer trivial ya que en los modelos hidrológicos se suelen utilizar datos externos como forzamiento. Sin embargo, los modelos hidrológicos se basan en un conocimiento a priori muy sólido: se supone que las ecuaciones son conocidas. Éste no es el caso en este estudio donde, por el contrario, las ecuaciones inicialmente son desconocidas. Este resultado es muy interesante ya que permite considerar la construcción de escenarios incluso cuando no se dispone de las ecuaciones que rigen los sistemas estudiados.
A partir de las concentraciones de CO2 y 222Rn, se obtuvieron otros modelos, los cuales destacan la existencia de un acoplamiento dinámico entre estas dos variables. El análisis de estos modelos reveló la naturaleza caótica de los sistemas subyacentes. La dinámica de la micro-atmósfera de la cueva está sincronizada principalmente con variaciones climáticas estacionales, y es muy próxima a un régimen caótico: una ligera alteración en la parametrización de los modelos obtenidos hace que la trayectoria converja hacia un atractor caótico (Fig.2A-2B). Estos son los primeros atractores caóticos de la dinámica atmosférica que provienen directamente de datos observacionales. Como era de esperar, su geometría difiere mucho del atractor obtenido por Lorenz en 1963 (Fig.2C-2D). Por un lado, esto se debe a que no resultan de la simplificación de un modelo idealizado como en el caso del sistema de Lorenz. Los modelos de la micro-atmósfera de Altamira se han obtenido directamente de observaciones, sin hipótesis a priori fuertes. Por otro lado, se inscriben en un contexto bastante específico, el de una cavidad subterránea, que involucra procesos tanto biológicos como físicos. Los modelos así obtenidos son, por supuesto, en sí mismos aproximaciones bastante burdas a la realidad, pero tienen una cierta capacidad predictiva (de aproximadamente un mes). Además, permiten resaltar el determinismo de baja dimensión subyacente y la proximidad a un régimen caótico. La imprevisibilidad de la naturaleza claramente no se puede reducir a un comportamiento puramente aleatorio.
Marina Sáez (Universidad de Alicante, CESBIO/OMP)
Sylvain Mangiarotti (CESBIO/OMP)
Soledad Cuezva (Universidad de Alcalá, España)
Ángel Fernández-Cortés (Universidad de Almería, España)
Beatriz Molero (CESBIO/OMP, France)
Sergio Sánchez-Moral (MNCN-CSIC, España)
David Benavente (Universidad de Alicante, España)
[i] Saltzman B., 1962. Finite Amplitude Free Convection as an Initial Value Problem—I., Journal of the Atmospheric Sciences, 19, 329–341.
[ii] Lorenz E.N., 1963. Deterministic nonperiodic flow, Journal of the Atmospheric Sciences, 20(2), 130-141.
[iii] Departamento de Ciencias de la Tierra y del Medio Ambiente (Universidad de Alicante, España) / Centre d’Études Spatiales de la Biosphère (CESBIO-OMP, UT3-CNRS-CNES-IRD-INRAe, Toulouse, France) / Departamento de geología, geografía y medio ambiente (Universidad de Alcalá, Madrid, Espagne) / Departamento de Biología y Geología (Universidad de Almería, España) / Museo Nacional de Ciencias Naturales (MNCN-CSIC, Madrid, España).
[iv] La herramienta GPoM, desarrollada en el Centre d’Etudes Spatiales de la Biosphère (Toulouse), tiene como objetivo obtener modelos de ecuaciones diferenciales directamente a partir de series temporales. https://insu.cnrs.fr/fr/cnrsinfo/est-il-possible-de-retrouver-les-equations-qui-gouvernent-la-dynamique-dun-systeme.
[v] Cuezva S, Fernandez-Cortes A, Benavente D, Serrano-Ortiz P, Kowalski A & Sanchez-Moral S, 2011. Short-term CO2 (g) exchange between a shallow karstic cavity and the external atmosphere during summer: role of the surface soil layer Atmospheric Environment 45:1418-1427. https://doi.org/10.1016/j.atmosenv.2010.12.023
[vi] Mangiarotti S. & Huc M., 2019. Can the original equations of a dynamical behaviour be retrieved from observational time series? Chaos, 29, 023133. https://doi.org/10.1063/1.5081448
[vii] Estos resultados se publican en la revista Theoretical and Applied Climatology: M. Sáez, S. Mangiarotti, S. Cuezva, A. Fernández-Cortés, B. Molero, S. Sánchez-Moral & D. Benavente, Global models for 222Rn and CO2 concentrations in the Cave of Altamira, 2020. https://link.springer.com/article/10.1007/s00704-020-03440-9